このインストールは、ここから入手したLTspice64.msiをインストールして使っています。
操作に関する要点を列挙します。
- 編集はMのキーを押した後で、ドラックで移動範囲を指定した後にドラック移動し、左クリックで確定。(ESCで取りやめ)
- 移動状態で、Ctl+Rのショートカットで回転できる。
- 配置した部品の右クリックで、パラメタなど値を変更できる。
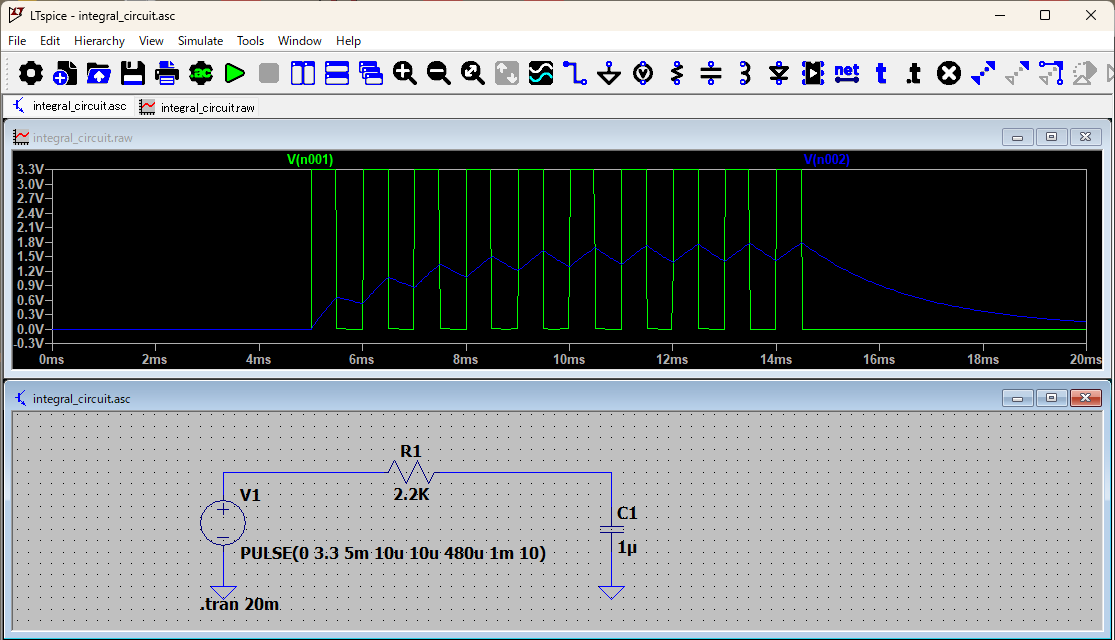
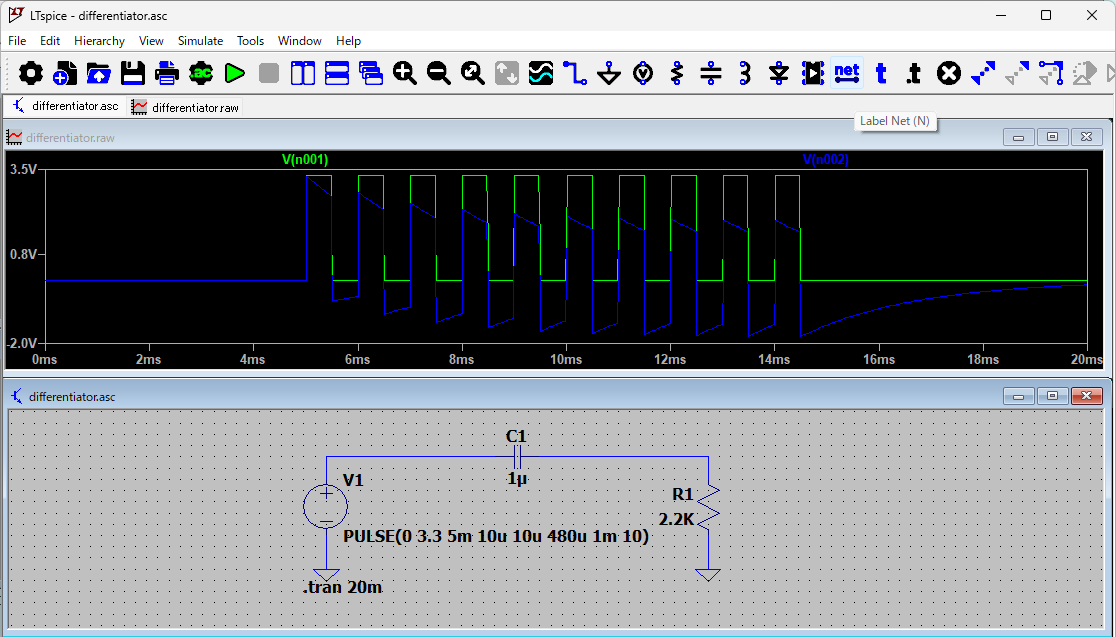
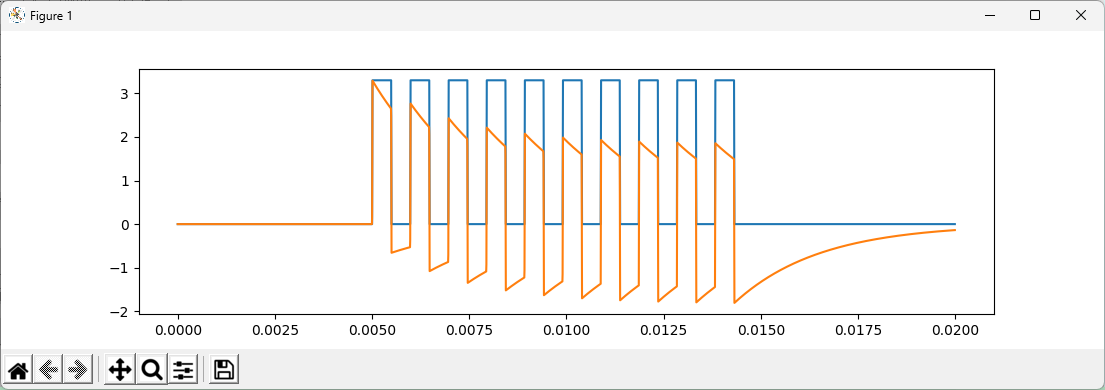
上記は、電源の右クリックで、Advanced クリックでPULSEにして以下の設定にした過渡特性です。
Vinitial:LOW電圧=0V Von:HIGH電圧=3.3V Tdelay:=2m Traise:立上り時間=10u秒 Tfall:立下り時間=10u秒 Ton:HIGH時間=480u秒(←HIGH電圧1Vの時間) Tperiod:周期=1m秒 Ncycle:10上記で使った部品名を変数とし、上記例であれば、R1=2.2KΩ、C1=1μFとしてプログラミングします。
電圧源変数をV1とし、コンデンサの端子電圧 Vc1とすると、
Vc1=1/ファラッド*クローン=1/ファラッド * ∫i(t)dt の定義より、 次の式がなり立ちます。
このクローンの電荷の変数をq1とすると、次のように考えるこよができます。
V1=R1*i + q1/C1 より、i=(V1-q1/C1)/R1 とiを求めることができます。
q1+=i*dt dtはシミュレーションで使う微小時間です。
q1をゼロから始めた以上の繰り返しで、過度特性のq1が求まり、Vc1=q1/C1で、コンデンサの端子電圧が求まられます。
以上の考え方で実現したコードを以下に示します。
import matplotlib.pyplot as plt
from typing import Callable
# 信号の変化を示すデータ
array=[(0,0), (5e-3,0),
(10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0), (10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0), (10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0),
(10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0), (10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0), (10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0),
(10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0), (10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0), (10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0),
(10e-6,3.3), (480e-6,3.3), (10e-6,0), (480e-6,0), (550e-6,0), ] # 各要素のtapleで[0]のデータが前の要素からの経過時間、[1] がその経過時の電圧値
def getSingnal(elapsed_time: float): # 外部リスト変数のarrayを参照し、経過時間から信号源のデータを得る
prev_cumul_time=array[0][0] # 繰り返しで、前の経過時間
prev_val=array[0][1]
i=1
len_array = len(array)
while i < len_array :
cumul_time = prev_cumul_time + array[i][0] # 経過時間
#print( i, cumul_time ,elapsed_time)
if cumul_time >= elapsed_time :
gradient=(array[i][1]-prev_val)/(array[i][0])
val=gradient*(elapsed_time-prev_cumul_time) + prev_val
return val
prev_cumul_time = cumul_time
prev_val=array[i][1]
i+=1
#
return array[i-1][1]
time_array=[v * 5e-6 for v in range(int(20e-3/5e-6))] # 過度特性の時間プロットデータ
val_array=[getSingnal(x) for x in time_array] # 回路の入力電圧のプロットデータ
plt.plot(time_array, val_array) # 入力源のデータをセット
# 積分回路のシミュレーション関数
def integral_circuit(getV1:Callable, time_array:list, R1:float , C1:float, q1=0 , dt=0.5e-6)->list:
'第1引数:getV1は経過時間を引数にしてその時の入力電圧を返す関数を登録するための引数'
'第2引数:time_arrayのリスト要素のタイミングで戻り値ので出力電圧のリストが作る'
'第3,4引数:R1は積分回路の抵抗値(単位はオーム)と、C1はコンデンサ(単位はファラット)'
'第5,6引数:q1はCに蓄えられた初期電荷(単位はクローン)と、dtはシミュレーションで使う微小時間(単位は秒)'
q1=0 # 初期電荷 0クローン
Vc1_list=[q1/C1]
time_idx=1
time_next=time_array[time_idx]
time_end=20e-3
time_now=0
while time_now < time_end:
v1=getV1(time_now)
i=(v1-q1/C1)/R1
q1+=i*dt
#print('-', end="")
if time_now > time_next:
#print(f"{time_idx:5}:{time_now:10.7f}, {q1/C1}v")
Vc1_list.append(q1/C1)
time_idx+=1
if time_idx >= len(time_array): break
time_next=time_array[time_idx]
time_now+=dt
return Vc1_list
Vc1_list = integral_circuit(getSingnal, time_array, R1=2.2e3 , C1=1e-6, q1=0 , dt=0.5e-6) # 積分回路の出力リスト
plt.plot(time_array, Vc1_list) # 積分回路の出力のプロット
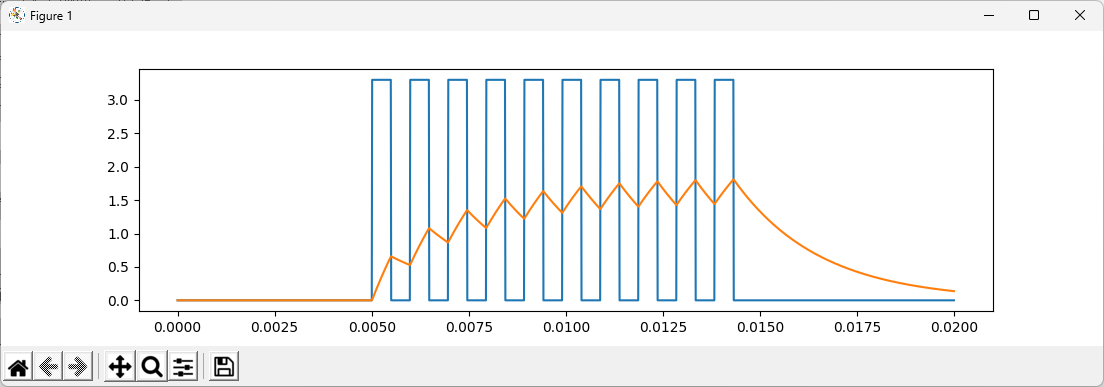
plt.show()
以下が実行結果のグラフです。