pythonメニュー
NumPyでのニューラルネットワーク1
単純パーセプトロン
単純パーセプトロンは、複数の入力(0または1)を受け取り、一つの出力((0または1)するもので、
x1, x2にの入力があり、それそれのyの出力に対する重みを、w1, w2 するとき、次式で表される。
(なお、thetaは閾値[しきいち]と呼ぶもので、yが1に変わる限界値を表現するものです。)
| y = | 0 となる条件 w1 * x1 + w2 * x2 <= theta |
| 1 となる条件 w1 * x1 + w2 * x2 > theta |
x1,x2,yは、「ニューロン」や[ノード]と呼ばれます。yが1に変化することは「ニューロンが発火する」と表現されます。
AND回路の実装例を示します。
上記式を前提に、さまざまものが実現できます。以下の例はAND回路の例で、(w1,w2,theta)のパラメタを適当に探した値です。
これは無限の組み合わせから(0.5, 0.5, 0.7)を適当に選んだ値です。
def AND(x1,x2): # AND回路の定義
w1,w2,theta=0.5, 0.5, 0.7
rv = x1*w1+x2*w2
if rv <= theta:
return 0
else:
return 1
AND(0,0)
AND(1,0)
AND(0,1)
AND(1,1)
バイアスを導入
パーセプトロンを表現する式を、バイアス b を導入して変形した例を示します。
| y = | 0 となる条件 b + w1 * x1 + w2 * x2 <= 0 |
| 1 となる条件 b + w1 * x1 + w2 * x2 > 0 |
この表現を、NumPy利用でANDを定義しなおした例を示します。
import numpy as np
def AND(x1,x2): # AND回路の定義
x = np.array( [x1, x2] )
w = np.array( [0.5, 0.5] )
b = -0.7
value = np.sum( w * x ) + b
if value <= 0:
return 0
else:
return 1
AND(0,0)
AND(1,0)
AND(0,1)
AND(1,1)
wの重きパラメタは、入力信号の重要度を表現するもで、bのバイアスパラメタは発火のしやすさ(出力を1にする度合い)を意味します。
NANDは、
wとbを変更するだけで、次のようにできます。
import numpy as np
def NAND(x1,x2): # NAND回路の定義
x = np.array( [x1, x2] )
w = np.array( [-0.5, -0.5] )
b = 0.7
value = np.sum( w * x ) + b
if value <= 0:
return 0
else:
return 1
NAND(0,0)
NAND(1,0)
NAND(0,1)
NAND(1,1)
ORも、
wとbを変更するだけで、次のようにできます。
import numpy as np
def OR(x1,x2): # OR回路の定義
x = np.array( [x1, x2] )
w = np.array( [0.5, 0.5] )
b = -0.2
value = np.sum( w * x ) + b
if value <= 0:
return 0
else:
return 1
OR(0,0)
OR(1,0)
OR(0,1)
OR(1,1)
多重パーセプトロンとは?
上記のように、
wとbを変更するだけでXOR回路を実現できるでしょうか?残念ながら単層パーセプトロンではできままん。
AND、NAND、OR回路は、線形式で可能ですが、非線形式が必要なXORでは、できないのです。
ですが、層を重ねれば非線形領域も表現可能になります。この考えが多重パーセプトロンです。
AND、NAND、OR回路を利用したXOR回路は、2層パーセプトロンで次ように実現できます。
def XOR(x1,x2): # XOR回路の定義
s1 = NAND( x1, x2 )
s2 = OR( x1, x2 )
y = AND( s1, s2 )
return y
XOR(0,0)
XOR(1,0)
XOR(0,1)
XOR(1,1)
x1,x2の入力である
0層、x1,x2を入力してs1,s2が得られる
1層、s1,s2を入力してyが得られる
2層で構成されるのが
2層パーセプトロンです。
多重パーセプトロンからニューラルネットワークへ
活性化関数(activation function)
パーセプトロンを表現する式を再び、示します(上記 ANDなそと同じ)
まず、単純パーセプトロンを汎用化した式に変形した訳です。
| y = | 0 となる条件 b + w1 * x1 + w2 * x2 <= 0 |
| 1 となる条件 b + w1 * x1 + w2 * x2 > 0 |
これを
活性化関数 を導入してシンプルな形に変形します。
| y = h(b + w1 * x1 + w2 * x2) |
| h(x) = | 0 となる条件 x<= 0 |
| 1 となる条件 x > 0 |
上記を活性化関数 h 導入するために、次のように分解します。
a = b + w1 * x1 + w2 * x2
y = h( a )
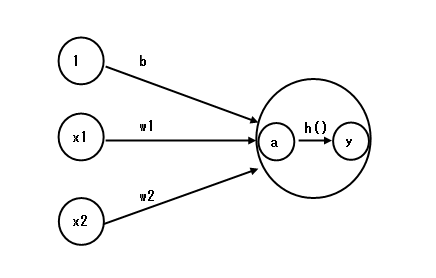
これをイメージ化した図を示します。
a のノードが、入力の重みを考慮した総和というノードです。
そして、
活性化関数 h()を使って、aから出力のyを求めるというわけです。
この式において、w1,w2を各入力層の影響の度合いで、
「重みパラメタ」と呼びます。
またbは、ニュローン発火のしやすさを表すもので、これを
「バイアス パラメタ」と呼びます。
ステップ関数の活性化関数
さて、これまでのパーセプトロンでは、活性関数に0か1の
ステップ関数を使っています。
ステップ関数は、次のような入出力です。
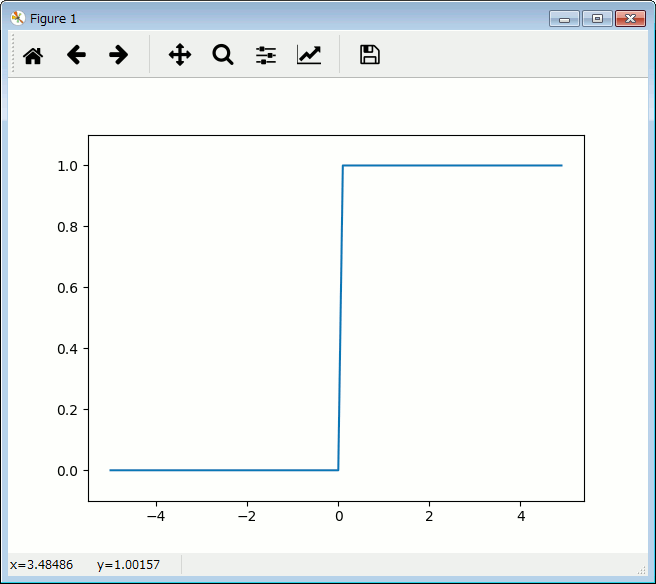
これは次のコードです。
import numpy as np
import matplotlib.pylab as plt
def step_function(x): # 活性関数として0か1になるステップ関数の定義
return np.array(x > 0,dtype=np.int)
x=np.arange(-5.0,5.0,0.1) # -5.0 〜 5.0の範囲を 0.1 のステップの配列を生成
y=step_function(x)
plt.plot(x,y) # プロット用データを設定
plt.ylim(-0.1, 1.1) # y軸の範囲設定
plt.show()
シグモイド関数の活性化関数
さて、これまでのパーセプトロンは活性関数に0か1の
ステップ関数を使ってしますが
シグモイド関数は、次のような入出力です。
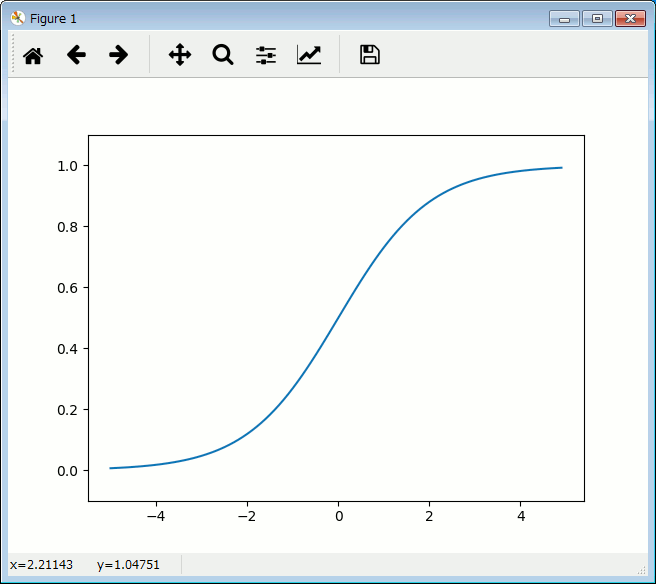
これは次のコードです。
def sigmoid(x): # 活性関数として0から1の滑らかな曲線で活性化させるシグモイド関数の定義
return 1 / (1 + np.exp(-x))
x=np.arange(-5.0, 5.0, 0.1)
y=sigmoid(x)
plt.plot(x,y)
plt.ylim(-0.1, 1.1) #y軸の範囲を指定
plt.show()
ReLU(Rectified Linear Unit:正規化線形関数)の活性化関数

これは次のコードです。
def relu(x):
return np.maximum(0,x)
x=np.arange(-5.0, 5.0, 0.1)
y=relu(x)
plt.plot(x,y)
plt.ylim(-0.1, 1.1) #y軸の範囲を指定
plt.show()
多重パーセプトロンからニューラルネットワーク(2層ニューラルネットワーク)へ
下記は、活性化関数 h()を使った単純パーセプトロン使って多重パーセプトロンにした構造です。
まず、
入力層(0層)が2つのニューロンで構成されています。
そして、それらを入力とした活性化関数「上記に示している h()」を使ったニューロンを3つ使っ
た第1層(一つ目の隠れ層)があります。
そして、それらを入力としたニューロンを2つ使う
第2層(2つ目の隠れ層)があります。
そして、それらを入力とした2つ出力があ
る第3層の出力層で構成されています。
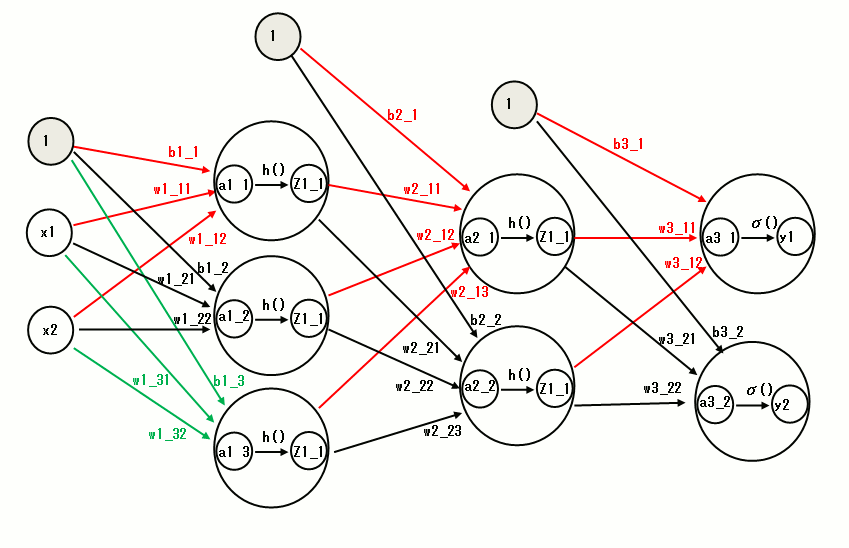
上記のニューラルネットワーク図において、活計化関数h()にシグモイド関数(sigmoid)を使って実装した例を次に示します。
なお上記では入力層と出力層以外に、2つの層がありますが、1層,2層と数えて、以降でこの構造を
2層ニューラルネットワークと呼びます。
# coding: UTF-8
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):# 活性関数として0から1の滑らかな曲線で活性化させるシグモイド関数の定義
return 1 / (1 + np.exp(-x))
print("1層目の算出 x1,x2の2つ入力からニューロン(a1_1,a1_2,a1_3)の出力A1を算出");
x1,x2=1.0, 0.5 # 2つ入力
w1_11, w1_21, w1_31= 0.1, 0.3, 0.5 #x1の入力に対する1層目各ニューロンの算出用重みパラメタ
w1_12, w1_22, w1_32= 0.2, 0.4, 0.6 #x2の入力に対する1層目各ニューロンの算出用重みパラメタ
b1_1, b1_2, b1_3= 0.1, 0.2 ,0.3
X=np.array( [ x1, x2 ] )
W1=np.array( [ [ w1_11, w1_21, w1_31 ] , [ w1_12, w1_22, w1_32 ] ])
B1=np.array( [ b1_1, b1_2, b1_3 ] )
A1=np.dot( X , W1 ) + B1
Z1=sigmoid(A1)
print(A1) # 表示結果: [ 0.3 0.7 1.1]
print(Z1) # 表示結果: [ 0.57444252 0.66818777 0.75026011]
print("\n\n 2層目の算出 (a1_1,a1_2,a1_3)ののA1のニューロンからAニューロン(a2_1,a2_2)の出力2を算出");
w2_11, w2_21= 0.1, 0.4 #A1[0]の入力に対する2層目各ニューロンの算出用重みパラメタ
w2_12, w2_22= 0.2, 0.5 #A1[1]の入力に対する2層目各ニューロンの算出用重みパラメタ
w2_13, w2_23= 0.3, 0.6 #A1[2]の入力に対する2層目各ニューロンの算出用重みパラメタ
b2_1, b2_2= 0.1, 0.2
W2=np.array( [ [ w2_11, w2_21 ] , [ w2_12, w2_22 ] , [ w2_13, w2_23 ] ])
B2=np.array( [ b2_1, b2_2 ] )
A2=np.dot( Z1 , W2 ) + B2
Z2=sigmoid(A2)
print(A2) # 表示結果: [ 0.51615984 1.21402696]
print(Z2) # 表示結果: [ 0.62624937 0.7710107 ]
print("\n\n 3層目の算出 (a2_1,a2_2)ののA2のニューロンからニューロン(a3_1,a3_2)の出力A3を算出");
w3_11, w3_21= 0.1, 0.3 #A2[0]の入力に対する3層目各ニューロンの算出用重みパラメタ
w3_12, w3_22= 0.2, 0.4 #A2[1]の入力に対する3層目各ニューロンの算出用重みパラメタ
b3_1, b3_2= 0.1, 0.2
W3=np.array( [ [ w3_11, w3_21 ] , [ w3_12, w3_22 ] ])
B3=np.array( [ b3_1, b3_2 ] )
A3=np.dot( Z2 , W3 ) + B3
Y=A3
print(Y) # 表示結果: [ 0.31682708 0.69627909]
上記を、クラスを使って書き直しました。
この時、ニューラルネットワークの慣例として、
「重みパラメタ」の辞書キーワードに「W」を文字を使いました。
バイアスには小文字「b」を使っています。
そして、これら辞書キーの接頭辞に入力層を除いたの番号を使います。
つまり、1層目が「W1,b1」、2層目が「W2,b2」,出力層が「W3,b3」のキー名を使います。
それを下記に示します。
# coding: UTF-8
import numpy as np
def sigmoid(x):# 活性関数として0から1の滑らかな曲線で活性化させるシグモイド関数の定義
return 1 / (1 + np.exp(-x))
class ForwardProc: # 順方向の伝搬(forward propagation)のニューラルネットワーク推論クラス
def __init__(self):
self.params = {} #データ管理用の辞書型初期化
# 1層目の重みと、バイアスパラメタの初期化
w1_11, w1_21, w1_31= 0.1, 0.3, 0.5 #x1の入力に対する1層目各ニューロンの算出用重みパラメタ
w1_12, w1_22, w1_32= 0.2, 0.4, 0.6 #x2の入力に対する1層目各ニューロンの算出用重みパラメタ
b1_1, b1_2, b1_3= 0.1, 0.2 ,0.3
self.params['W1']=np.array( [ [ w1_11, w1_21, w1_31 ] , [ w1_12, w1_22, w1_32 ] ])
self.params['b1']=np.array( [ b1_1, b1_2, b1_3 ] )
# 2層目の重みと、バイアスパラメタの初期化
w2_11, w2_21= 0.1, 0.4 #A1[0]の入力に対する2層目各ニューロンの算出用重みパラメタ
w2_12, w2_22= 0.2, 0.5 #A1[1]の入力に対する2層目各ニューロンの算出用重みパラメタ
w2_13, w2_23= 0.3, 0.6 #A1[2]の入力に対する2層目各ニューロンの算出用重みパラメタ
b2_1, b2_2= 0.1, 0.2
self.params['W2']=np.array( [ [ w2_11, w2_21 ] , [ w2_12, w2_22 ] , [ w2_13, w2_23 ] ])
self.params['b2']=np.array( [ b2_1, b2_2 ] )
# 3層目(出力)の重みと、バイアスパラメタの初期化
w3_11, w3_21= 0.1, 0.3 #A2[0]の入力に対する3層目各ニューロンの算出用重みパラメタ
w3_12, w3_22= 0.2, 0.4 #A2[1]の入力に対する3層目各ニューロンの算出用重みパラメタ
b3_1, b3_2= 0.1, 0.2
self.params['W3']=np.array( [ [ w3_11, w3_21 ] , [ w3_12, w3_22 ] ])
self.params['b3']=np.array( [ b3_1, b3_2 ] )
def predict(self,x): # 予測関数
W1,W2,W3=self.params['W1'],self.params['W2'],self.params['W3']
b1,b2,b3=self.params['b1'],self.params['b2'],self.params['b3']
a1=np.dot( x , W1 ) + b1
z1=sigmoid(a1)
print(a1), print(z1) # =============表示結果
a2=np.dot( z1 , W2 ) + b2
z2=sigmoid(a2)
print(a2) , print(z2) # =============表示結果
a3=np.dot( z2 , W3 ) + b3
y=a3 # 出力層
return y
network=ForwardProc()
x=np.array( [ 1.0, 0.5 ] ) # 2つ入力
y=network.predict(x)
print(y) # 表示結果: [ 0.31682708 0.69627909]
以上のようにクラス化して、
の部分のように重みとバイアスパラメタを取得して計算できるようにしました。
そうすれば、例えば層の入力が784個の入力、1層目が50個、2層目が100個、3層目が10個のニューウロン数 と変わった場合でも、
xが[784,0]、W1が[785,50]、W2が[50,100]、W2が[100,10]のNumpy配列で得られるように初期するだけで、
predict関数を変更しなくても使えます。
出力層で使う恒等関数やソフトマックス関数
前述のコードで、出力層を求める最後の算出で「
y=a3 」と行っています。
これは出力層ニューロン内の「
δ()」で表現するものを実装したものですが、単なる代入なので、
入力値に対して、何も手を加えないで出力しているので、「
恒等関数」と呼ばれます。
対して、出力の総和が1となって、個々の出力が予想確率となる関数が「
ソフトマックス関数」と呼ばれます。
「
ソフトマックス関数」は次のように定義されます。
| 基本式 | オーバフロー対策したコード |
def softmax(a):
exp_a=np.exp(a)
sum_exp_a = np.sum( exp_a )
y=exp_a/sum_exp_a
return y
|
def softmax(a):
c=np.max(a)
exp_a=np.exp(a-c) #オーバフロー対策
sum_exp_a = np.sum( exp_a )
y=exp_a/sum_exp_a
return y
|
前述のForwardProcクラスのpredictメソッド最後の「
恒等関数」に相当する「
y=a3 」を、
「
softmax(a3) 」に変更すると、
最後の出力print(y)は、「[ 0.40625907, 0.59374093 ]」となります。
これは入力に対して、 0.40625907の確率でy1のニューロンが発火し、0.59374093の確率でy2のニューロンが発火することを意味し、
これが、ニューラルネットワークの推論処理の結果です。
( なお、0.40625907+0.59374093=1の関係です。)
ニューラルネットワークは「分類問題」と「回帰問題」で使われます。
「分類問題」とは、データがどれに属するかを問う問題で、一般に出力層に「ソフトマックス関数」が使われます。
「回帰問題」とは、連続的データに使われ、出力の結果の値を予想するような問題で、
一般に出力層に「恒等関数」が使われます。
前述の例(ForwardProcクラス)は、1つ(入力層が2つ[ 1.0, 0.5 ] )の入力の例ですが、実際に使う場合は、沢山のデータを一括して行わせるのが普通です。
この沢山のデータを一括して行わせる処理は、バッチ処理と呼ばれます。
numpyのライブラリは処理時間を短縮するために、配列の計算処理を効率的にできるように最適化されているので、
その能力を利用するための処理とも言えますが、バッチ処理に対応できるような対策も必要となります。
具体例を、前述で定義したsoftmax関数を例に示します。出力層が2つで「0.4, 0.6」の出力を引数にして実行すると次のようになります。
>>> softmax(np.array([0.4, 0.6]))
array([ 0.450166, 0.549834])
これで得られた[ 0.450166, 0.549834]が入力が各出力と予想した分類の確率を意味していました。
さて、バッチ処理で2件分を一括処理した例を示します。「[ [0.4, 0.6], [0.7, 0.5] ]」の入力です。
>>> softmax( np.array([ [0.4, 0.6], [0.7, 0.5] ]) )
array([[ 0.21383822, 0.26118259], 正しくない結果であることが、すぐわかります。これは、softmax関数がバッチ処理に対応していないからです。
[ 0.28865141, 0.23632778]])
以下にバッチ処理に対応するよう修正しした関数と実行させた例を示します。
def softmax(x):
if x.ndim == 2: # バッチ処理の引数データか?
x = x.T # 転置行列を求る。
x = x - np.max(x, axis=0) # オーバーフロー対策
y = np.exp(x) / np.sum(np.exp(x), axis=0) # axis=0で、内部配列ごとに処理
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
>>> softmax( np.array([ [0.4, 0.6], [0.7, 0.5] ]) )
array([[ 0.450166, 0.549834],
[ 0.549834, 0.450166]])
>>>
このsoftmax関数を利用して、前述の例(ForwardProcクラス)をバッチ処理するものに変更しました。
その例を下記に示します。
これは入力層のノード数が784個あり、そのテスト用データ(1つが784個の情報)が1000個ある例で、出力が10個ある例です。
中間層は3層で、重みとバイアスのパラメタが学習済として、pickleで直列化したファイル('weight_bias_params_0.pkl')が用意用意されており、
コンストラクタ(__init__)内で、読み取って辞書に記憶させています。
辞書は上記例と同じで'W1','W2','W3'が各層の重みで、'b1','b2','b3'がバイアスです。
(1層目のニューロン数が50、2層目のニューロン数が100,3層目のニューロン数が10)
また、入力用テストデータとその解答ラベルが10000個が、それぞれ(x_test.pkl,t_test.pkl)用意されており、
そのテストデータを100個のバッチ数ごとに推測し、その結果と解答ラベルが一致している割合(比率)を出力しているコードです。
# coding: UTF-8
# src=forward_proc_bat.py
import numpy as np
import pickle
def sigmoid(x):# 活性関数として0から1の滑らかな曲線で活性化させるシグモイド関数の定義
return 1 / (1 + np.exp(-x))
def softmax(x): # バッチ対応版
if x.ndim == 2: # バッチ処理の引数データか?
x = x.T # 転置行列を求る。
x = x - np.max(x, axis=0) # オーバーフロー対策
y = np.exp(x) / np.sum(np.exp(x), axis=0) # axis=0で、内部配列ごとに処理
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
class ForwardProc: # 順方向の伝搬(forward propagation)のニューラルネットワーク推論クラス
def __init__(self):
# 重みとバイアスのパラメタが学習済として、そのpickleで直列化したファイル('weight_bias_params_0.pkl')から復元
with open('weight_bias_params_0.pkl', mode='rb') as fr:
self.params = pickle.load( fr ) # 復元する
def predict(self,x): # 予測関数
W1,W2,W3=self.params['W1'],self.params['W2'],self.params['W3']
b1,b2,b3=self.params['b1'],self.params['b2'],self.params['b3']
a1=np.dot( x , W1 ) + b1
# print(a1.shape) # =============表示結果: (50,)
z1=sigmoid(a1)
a2=np.dot( z1 , W2 ) + b2
# print(a2.shape) # =============表示結果:(100,)
z2=sigmoid(a2)
a3=np.dot( z2 , W3 ) + b3
y = softmax(a3) # 出力層
return y
network=ForwardProc()
print("W1:" , network.params['W1'].shape) # =============表示結果: W1 (784, 50)
print("b1:" , network.params['b1'].shape) # =============表示結果: b1: (50,)
print("W2:" , network.params['W2'].shape) # =============表示結果: W2: (50.100)
print("b2:" , network.params['b2'].shape) # =============表示結果: b2: (100,)
print("W3:" , network.params['W3'].shape) # =============表示結果: W3: (100,10)
print("b3:" , network.params['b3'].shape) # =============表示結果: b3: (10,)
with open('x_test.pkl', mode='rb') as fr:
x = pickle.load( fr ) # テスト用データのオブジェクトを復元する
with open('t_test.pkl', mode='rb') as fr:
t = pickle.load( fr ) # テスト用ラベルのオブジェクトを復元する 解答ラベルt[0]がx[0]のデータの分類用識別値
# ----------------------------------------------------------------
# 10000件を100個のバッチ数ごとに推測し、その結果と解答ラベルが一致している割合(比率)を出力している。
batch_size=100
accuracy_cnt = 0 # x[0]の処理結果(10,)のy最大確率値の位置が 解答ラベルt[0]であれば正解できたと判断して、それを計数する。
for i in range(0, len(x), batch_size):
x_batch = x[i:i+batch_size]
y_batch = network.predict( x_batch )
p= np.argmax(y_batch, axis=1) # 各配列で最も確率の高い要素のインデックスを取得
accuracy_cnt += np.sum( p == t[i:i+batch_size] )
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
052から060行がバッチ処理ですが、このくらい数程度ならバッチ処理でなくても可能です。参考に単なる繰り返しと一括処理も示します。
# ----------------------------------------------------------------
# バッチ処理でなく、テストデータの10000件を1つずつ繰り返しで推測し、その結果と解答ラベルが一致している割合(比率)を出力している。
accuracy_cnt = 0
for i in range(len(x)):
y = network.predict( x[i])
p= np.argmax(y) # 最も確率の高い要素のインデックスを取得
if p == t[i]:
accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
# ----------------------------------------------------------------
# 10000を一括して処理した場合の例
y=network.predict(x)
p= np.argmax(y, axis=1) # 各配列で最も確率の高い要素のインデックスを取得
accuracy_cnt = np.sum( p == t )
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
 これをイメージ化した図を示します。
これをイメージ化した図を示します。


