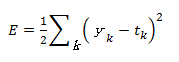
def mean_squared_error(y,t):
return 0.5 * np.sum((y-t)**2)
mean_squared_error( y, t_train[0] ) # 結果 0.05029471401664868
この値が小さいので、「重みとバイアスのパラメタ」の設定が適切! のような判定に使う訳です。結果は、0から1.0の結果です。
NumPyでのニューラルネットワーク1の続きです。
前回は、ニューラルネットワークの学習済みパラメタ「重みとバイアス」を使って、その信憑性をテストしました。
今回は、パラメタ「重みとバイアス」をどのように作るか?(学習させるか)の内容です。
1エポック(epoch)で、すべての訓練データデータを参照したこと意味する単位である。 学習においては、この単位ごとに「バイアスと重み」の解を計算させる手法がよく使われる。
一般に、訓練データ,訓練ラベル(訓練用教師ラベル)を使って、パラメタ「重みとバイアス」を探します。
この方法が、最も重要なところですが、ここでは最も基本とされる「確率的勾配降下法(SGD:stochastic grandient descent)」を紹介します。
これは、無造作に選んだパラメタ「重みとバイアス」に対して予想させ、その予想値と訓練ラベルの差の勾配から、より差がなくなるように
パラメタ「重みとバイアス」を修正する繰り返しで行います。
その後、学習で得られたされたパラメタ「重みとバイアス」で、テストデータ,テストラベル(テスト用教師ラベル)を評価して、
前のページ で行ったような信憑性をテストします。
yの出力: [ 1.06677078e-02 1.58301147e-04 4.30344051e-04 2.15528250e-01 5.69069698e-06 7.67599761e-01 3.01648834e-05 3.11577786e-03 1.66547787e-03 7.98536697e-04]この上記データは、ソフトマックス関数の出力なので、10個の分類に対するそれぞれを予想する確率の値です。
tの正解: [ 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]この2つの配列から、どれだけ予想が合わないかの損失関数を求めている訳です。
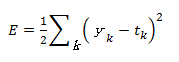
def mean_squared_error(y,t):
return 0.5 * np.sum((y-t)**2)
mean_squared_error( y, t_train[0] ) # 結果 0.05029471401664868
この値が小さいので、「重みとバイアスのパラメタ」の設定が適切! のような判定に使う訳です。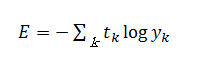
def cross_entropy_error(y,t):
delta = 1e-7
return -np.sum( t * np.log(y+delta) )
cross_entropy_error( y, t_train[0] ) # 結果 0.26448667049407959
目安として、出力の正解要素の確率が0.6で-log0.6=0.51、、出力の正解要素の確率が0.1と性能が悪い例で-log0.1=2.3となります。
def cross_entropy_error(y, t): # 交差エントロピー誤差取得
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 教師データが one-hot-vector の場合、正解ラベルのインデックスに変換
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size # バッチサイズは、グローバルで与える。
コンストラクタ:入力層の数、出力層の数、学習率用のハイパーパラメタを引数にして、「重みとバイアスのパラメタ」乱数を設定する指定と 過去の学習済みファイルを指定する方法の23通りの使い方が可能。
predict: 各出力層の確率を返す
loss: 上記交差エントロピー誤差を利用して、訓練データの入力のxに対して、,訓練ラベル(訓練用教師ラベル1)の損失を計算して返す。
''' ファイル名: two_layer_net0.py '''
import numpy as np
import pickle
def numerical_gradient(f, x): # 関数fの勾配を、x の勾配を求める
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 値を元に戻す
it.iternext()
return grad
def sigmoid(x): # 活性関数として0から1の滑らかな曲線で活性化させるシグモイド関数の定義
return 1 / (1 + np.exp(-x))
def softmax(x):
if x.ndim == 2: # バッチ処理の引数データか?
x = x.T # 転置行列を求る。
x = x - np.max(x, axis=0) # オーバーフロー対策
y = np.exp(x) / np.sum(np.exp(x), axis=0) # axis=0で、内部配列ごとに処理
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
def cross_entropy_error(y, t): # 交差エントロピー誤差取得
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 教師データが one-hot-vector の場合、正解ラベルのインデックスに変換
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size # バッチサイズは、グローバルで与える。
class TwoLayerNet: # 2層の深層学習用クラス
# コンストラクタ
def __init__(self, input_size=784, hidden_size=50, output_size=10, weight_init_std=0.01, file=""):
if file != "":
with open(file, mode='rb') as fr:
self.params = pickle.load( fr ) # 復元する
return
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 予測して、各出力層の確率を返す
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
#
# x:入力データ, t:教師データ
def loss(self, x, t): # xの訓練データと、tの正解ラベルから、その差を誤差をして返す損失関数
y = self.predict(x) # 上記で説明!
return cross_entropy_error(y, t)
#
def numerical_gradient(self, x, t):# x:入力データ, t:教師データ 損失との勾配を求める。
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
#
# paramsの保存
def save_params(self, file='weight_bias_params_0.pkl'):
with open(file, mode='wb') as fw:
pickle.dump(self.params, fw) # 直列化 (Serialize) して保存
#
from two_layer_net0 import TwoLayerNet
import pickle
import numpy as np
import matplotlib.pyplot as plt
plt.figure() # 2次元の図を初期化「1つshow()の前に必要」
np.random.seed(420)
# 訓練用データの読み込み
with open('x_train.pkl', mode='rb') as fr: # 1つが[784]byteという入力データが、複数並ぶ訓練データを取得(このファイルはこれで取得)
x_train=pickle.load( fr)
with open('t_train_a.pkl', mode='rb') as fr: # 上記の並びに対応する教師ラベル(1つがone-hot表現で10個の出力)が、複数並ぶ訓練データを取得
t_train=pickle.load( fr)
train_size = x_train.shape[0] # 訓練データサイズ:60000
train_size = 100
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)#学習用のニューラルネットワーク生成
batch_size = 10
learning_rate = 0.1 # 学習率
iters_num = 1000 # 勾配法の算出繰り返しの回数
train_loss_list = [] #予測と(訓練用教師ラベル)の損失
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask] # batch_maskの添え字群で指定される訓練データ群を抽出
t_batch = t_train[batch_mask] # batch_maskの添え字群で指定される訓練データ群の訓練ラベル(訓練用教師ラベル)を抽出
#
# ここを有効にすると、最初の訓練に使われる画像と正解ラベルが確認できます。'
# print(x_batch[0]) # [0. 0. 0.・・784個・・. 0. 1. 0.]
# print(t_batch[0]) # [0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
# plt.imshow(x_batch[0].reshape((28,28)), "gray")
# plt.show()
# exit()
#
# 勾配の計算
grad = network.numerical_gradient(x_batch, t_batch)
# grad = network.gradient(x_batch, t_batch)
# print("勾配:",grad)
#
# 「重みとバイアスのパラメタ」を更新
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
#
loss = network.loss(x_batch, t_batch)
print(i, ":", loss)
train_loss_list.append(loss)
plt.plot(np.arange(len(train_loss_list)),np.array(train_loss_list), label="回数")
print("訓練データ数:", train_size);
print("バッチ数:", batch_size);
print("計算回数:", iters_num);
plt.show()
network.save_params() # ここで、学習過程を記録する
実行結果の例です。(この実行は、約6時間かかりました。)
>python two_layer_net_train0.py 0 : 2.2359410604331758 1 : 2.1760343971680407 2 : 2.234318482464327 ・・・・・ 992 : 0.10349291915839776 993 : 0.10499616243219019 994 : 0.09725474712539708 995 : 0.0498439587858408 996 : 0.0773463562908289 997 : 0.16144745019785683 998 : 0.0334531657318317 999 : 0.1161840789493219 訓練データ数: 100 バッチ数: 10 計算回数: 1000
上記の学習において得られた重みとバイアスパラメタが'weight_bias_params_0.pkl'に記憶されており、
それをコンストラクタでロードして、 params['W1']、 params['b1']、 params['W2']、 params['b2']にリストアします。
それで、テストデータをチェックのために判定するコードを以下に示します。
('weight_bias_params_0.pkl'は、ここからダウンロードできます。)
from two_layer_net0 import TwoLayerNet
import pickle
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
network = TwoLayerNet(file='weight_bias_params_0.pkl')#学習用のニューラルネットワーク生成
print("W1:" , network.params['W1'].shape) # =============表示結果: W1 (784, 50)
print("b1:" , network.params['b1'].shape) # =============表示結果: b1: (50,)
print("W2:" , network.params['W2'].shape) # =============表示結果: W2: (50.10)
print("b2:" , network.params['b2'].shape) # =============表示結果: b2: (10,)
with open('x_train.pkl', mode='rb') as fr:
x_train = pickle.load( fr ) # 訓練用データのオブジェクトを復元する
with open('t_train_a.pkl', mode='rb') as fr:
t_train = pickle.load( fr ) # 訓練用ラベルのオブジェクトを復元する
while True:
print("検証画像数:", x_train.shape[0] )
idx = input("検証したい画像の添え字>>")
if idx == "": break
idx=int(idx)
#
y = network.predict( x_train[idx] )
print("yの出力:", y)
n = np.argmax(y)
print("予測した値:", n)
print("tの正解:", t_train[idx] )
plt.imshow(x_train[idx].reshape((28,28)), "gray")
plt.show()
>>python two_layer_net_predict0.py W1: (784, 50) b1: (50,) W2: (50, 10) b2: (10,) 検証画像数: 60000 検証したい画像の添え字>>6 yの出力: [0.12547638 0.19049372 0.06153873 0.0814133 0.06678886 0.04027311 0.14453269 0.06058082 0.09024332 0.13865907] 予測した値: 1 tの正解: [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] 検証画像数: 60000 検証したい画像の添え字>>50000 yの出力: [0.08465715 0.10089443 0.10245315 0.10062295 0.09982012 0.09073989 0.09922095 0.09874611 0.12491723 0.09792801] 予測した値: 8 tの正解: [0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]最初の画像選択キー入力で 6 を選択した場合、1と判定できる確率が0.19049372と最も多く、予測値として 1 は、1. の位置と合って、正しい判断と分かります。
''' ファイル名: two_layer_net.py '''
import numpy as np
import pickle
def sigmoid(x): # 活性関数として0から1の滑らかな曲線で活性化させるシグモイド関数の定義
return 1 / (1 + np.exp(-x))
def sigmoid_grad(x):
return (1.0 - sigmoid(x)) * sigmoid(x)
def softmax(x):
if x.ndim == 2: # バッチ処理の引数データか?
x = x.T # 転置行列を求る。
x = x - np.max(x, axis=0) # オーバーフロー対策
y = np.exp(x) / np.sum(np.exp(x), axis=0) # axis=0で、内部配列ごとに処理
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
def cross_entropy_error(y, t): # 交差エントロピー誤差取得
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 教師データが one-hot-vector の場合、正解ラベルのインデックスに変換
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t])) / batch_size # バッチサイズは、グローバルで与える。
class TwoLayerNet:
# コンストラクタ
def __init__(self, input_size=784, hidden_size=50, output_size=10, weight_init_std=0.01, file=""):
if file != "":
with open(file, mode='rb') as fr:
self.params = pickle.load( fr ) # 復元する
return
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
#
# 予測して、各出力層の確率を返す
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
#
# x:入力データ, t:教師データ
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y, t)
#
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
#
def gradient(self, x, t): # x:入力データ, t:教師データ 損失との勾配を求める。(誤差逆伝搬法)
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
grads = {}
batch_num = x.shape[0]
# forward
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
# backward
dy = (y - t) / batch_num
grads['W2'] = np.dot(z1.T, dy)
grads['b2'] = np.sum(dy, axis=0)
#
da1 = np.dot(dy, W2.T)
dz1 = sigmoid_grad(a1) * da1
grads['W1'] = np.dot(x.T, dz1)
grads['b1'] = np.sum(dz1, axis=0)
return grads
#
# paramsの保存
def save_params(self, file='weight_bias_params_0.pkl'):
with open(file, mode='wb') as fw:
pickle.dump(self.params, fw) # 直列化 (Serialize) して保存
import pickle
import numpy as np
from two_layer_net import TwoLayerNet
import matplotlib.pyplot as plt
plt.figure() # 2次元の図を初期化「1つshow()の前に必要」
np.random.seed(420)
# 訓練用データの読み込み
with open('x_train.pkl', mode='rb') as fr: # 1つが[784]byteという入力データが、複数並ぶ訓練データを取得
x_train=pickle.load( fr)
with open('t_train_a.pkl', mode='rb') as fr: # 上記の並びに対応する教師ラベル(1つがone-hot表現で10個の出力)が、複数並ぶ訓練データを取得
t_train=pickle.load( fr)
train_size = x_train.shape[0] # 訓練データサイズ:60000
train_size = 10000
train_size = 1000
network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)#学習用のニューラルネットワーク生成
batch_size = 100
batch_size = 10
learning_rate = 0.1 # 学習率
iters_num = 10000 # 勾配法の算出繰り返しの回数
iters_num = 1000 # 勾配法の算出繰り返しの回数
train_loss_list = [] #予測と(訓練用教師ラベル)の損失
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask] # batch_maskの添え字群で指定される訓練データ群を抽出
t_batch = t_train[batch_mask] # batch_maskの添え字群で指定される訓練データ群の訓練ラベル(訓練用教師ラベル)を抽出
#
# ここを有効にすると、最初の訓練に使われる画像と正解ラベルが確認できます。'
# print(x_batch[0]) # [0. 0. 0.・・784個・・. 0. 1. 0.]
# print(t_batch[0]) # [0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
# plt.imshow(x_batch[0].reshape((28,28)), "gray")
# plt.show()
# exit()
#
# 勾配の計算
grad = network.gradient(x_batch, t_batch) # network.numerical_gradientの代わりの高速版
# 「重みとバイアスのパラメタ」を更新
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
#
loss = network.loss(x_batch, t_batch)
print(i, ":", loss)
train_loss_list.append(loss)
plt.plot(np.arange(len(train_loss_list)),np.array(train_loss_list), label="回数")
print("訓練データ数:", train_size);
print("バッチ数:", batch_size);
print("計算回数:", iters_num);
plt.show()
network.save_params()
from two_layer_net import TwoLayerNet
import pickle
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(420)
network = TwoLayerNet(file='weight_bias_params_0.pkl')#学習用のニューラルネットワーク生成
print("W1:" , network.params['W1'].shape) # =============表示結果: W1 (784, 50)
print("b1:" , network.params['b1'].shape) # =============表示結果: b1: (50,)
print("W2:" , network.params['W2'].shape) # =============表示結果: W2: (50.10)
print("b2:" , network.params['b2'].shape) # =============表示結果: b2: (10,)
with open('x_train.pkl', mode='rb') as fr:
x_train = pickle.load( fr ) # 訓練用データのオブジェクトを復元する
with open('t_train_a.pkl', mode='rb') as fr:
t_train = pickle.load( fr ) # 訓練用ラベルのオブジェクトを復元する
while True:
print("検証画像数:", x_train.shape[0] )
idx = input("検証したい画像の添え字>>")
if idx == "": break
idx=int(idx)
#
y = network.predict( x_train[idx] )
print("yの出力:", y)
n = np.argmax(y)
print("予測した値:", n)
print("tの正解:", t_train[idx] )
plt.imshow(x_train[idx].reshape((28,28)), "gray")
plt.show()