帿彂愭摢儁乕僕傊栠傞
僯偐傜巒傑傞忣曬張棟梡岅
00000116
2恑悢
00000250
擇暘扵嶕
00000628
擇暘朄
00000627
僯儏乕僩儞朄
00000621
恖娫偺張棟擻椡
00000156
擣徹嬊
僶僀僫儕忣曬傪昞尰偡傞曽朄偺堦偮偱丄俀傪婎悢偲偡傞昞尰
戝偒偔偼晞崋側偟2恑悢乮晞崋側偟惍悢乯偲丄晞崋晅偒2恑悢乮晞崋晅偒惍悢乯偵暘偗傜傟傞丅
仠晞崋側偟2恑悢乮晞崋側偟惍悢乯
椺
俀恑悢偺1010丂偼丂丂
1亊2偺俁忔 + 0亊2偺俀忔 + 1亊2偺侾忔 + 0亊2偺侽忔
= 1亊8丂丂 + 0亊4 + 1亊2 + 0亊1
= 8 + 0 + 2 + 0
=10
偮傑傝丄俀恑悢偺1010丂偼丂10傪堄枴偡傞抣偵側傞丅
媡曄姺偡傞応崌偼丄師偺傛偆偵壓偺寘偐傜寁嶼偡傟偽傛偄丅
10偱偁傟偽丄
10傪丂2偱妱偭偨梋傝仺0丂丂丂丂仼嵟壓埵偺寘
偦偺彜偺5傪丂2偱妱偭偨梋傝仺1
偦偺彜偺2傪丂2偱妱偭偨梋傝仺0
偦偺彜偺1傪丂2偱妱偭偨梋傝仺1丂丂丂丂仼嵟忋埵偺寘
偦偺彜偼0丂丂丂偲彜偑0偵側傞傑偱寁嶼偡傟偽傛偄丅
乮彜偺嶼弌偼丄彫悢揰傪愗傝幪偰偰摼傞丅乯
4價僢僩慡偰偺慻傒崌傢偣傪10恑悢偱昞尰偡傞偲師偺傛偆偵側傞丅
0000丂仺丂0
0001丂仺丂1
0010丂仺丂2
0011丂仺丂3
0100丂仺丂4
0101丂仺丂5
0110丂仺丂6
0111丂仺丂7
1000丂仺丂8
1001丂仺丂9
1010丂仺丂10
1011丂仺丂11
1100丂仺丂12
1101丂仺丂13
1110丂仺丂14
1111丂仺丂15
俀恑悢偺壛嶼偼丄0+0仺0丄0+1仺1丄1+0仺1丄1+1仺1偱寘忋偑傝乮carry乯偑惗偠傞丂偺婯懃偱峴傢傟傞丅
椺
丂 01101010
丂 11101100
-----------壛嶼偡傞
丂101010110
仠晞崋晅偒2恑悢乮晞崋晅偒惍悢乯
晞崋晅偒2恑悢偼丄晧悢傪俀偺曗悢偱昞尰偡傞丅丂嵟忋埵價僢僩偑侾偺僨乕僞偼晧偺抣偵側傞丅
0000丂仺丂0
0001丂仺丂1
0010丂仺丂2
0011丂仺丂3
0100丂仺丂4
0101丂仺丂5
0110丂仺丂6
0111丂仺丂7
1000丂仺丂-8
1001丂仺丂-7
1010丂仺丂-6
1011丂仺丂-5
1100丂仺丂-4
1101丂仺丂-3
1110丂仺丂-2
1111丂仺丂-1
惓偺2恑悢偐傜晧偵曄姺偡傞乮俀偺曗悢偵曄姺偡傞乯曽朄偼丄
傑偢丄侾偺曗悢偵偟偐傜偦傟偵侾傪壛嶼偡傟偽傛偄丅
側偍丄1偺曗悢偵偡傞偵偼慡價僢僩偺0偲1傪媡偵偡傟偽傛偄丅
椺丂俆偺2恑悢0101傪丄-5偺1011偵偡傞偵偼丠
傑偢侾偺曗悢偵偡傞丅乮慡價僢僩傪媡乯
0101仺1010
1010偵1傪壛嶼偟偰丄1011偵側傞丅
媡偵晧偐傜惓傪媮傔傞応崌偼丄1堷偄偰偐傜斀揮偡傟偽傛偄偑丄
傑偨晧偵偡傞偲尦偺惓偵栠傞峫偊偱丄摨條偵慡價僢僩傪媡偵偟偰侾傪壛偊偰媮傔偰傕傛偄丅
側偍丄晧偺悢抣傪俀偺曗悢偱昞尰偡傞棟桼偼丄晧偺壛嶼傕惓偺壛嶼偺巇慻傒偱幚尰偱偒偙偲偱偁傞丅
壛嶼偺巇慻傒偼丄0+0仺0丄0+1仺1丄1+0仺1丄1+1仺1偱寘忋偑傝乮carry乯偑惗偠傞偱偁傞偑丄
偙偺巇慻傒偑偦偺傑傑揔梡偱偒傞丅
椺
6丂+丂(-5)傪媮傔傞帪丄
丂 0110
丂 1011
--------
丂10001
側偍丄愭摢偵惗傑傟偨寘忋偑傝偺價僢僩偼丄4價僢僩墘嶼偱偼懚嵼偟側偄價僢僩側偺偱柍帇偟偰寢壥偼侾偵側傞丅
攝楍偺僨乕僞偑惍楍偝傟偰偄傞乮戝偒偄弴偲偐丄彫偝偄弴偵側傜傫偱偄傞応崌偩偗巊偊傞乯
戙悢揑側夝朄偑巊偊側偄応崌偵巊傢傟傞庤朄偺堦偮偱丄摫娭悢偑媮傔傜傟側偄応崌偵傕巊偊傑偡丅
婎杮揑側峫偊曽
f(x1)偲f(x2)偱晞崋偑堎側傞俀偮偺倶傪巜掕偟偰丄嬫娫傪巜掕偟傑偡丅佀乮侾乯
偙偺嬫娫傪擇暘偟偰弌棃偨嬫娫乮俀乯丄乮俁乯偵偍偄偰丄偦偺椉抂偺f(x)偺晞崋偑堎側傞曽佀乮俀乯偵崻偑懚嵼偡傞偲偟偰丄崻偑偁傞嬫娫傪嫹傔偰峴偔庤朄偱偡丅
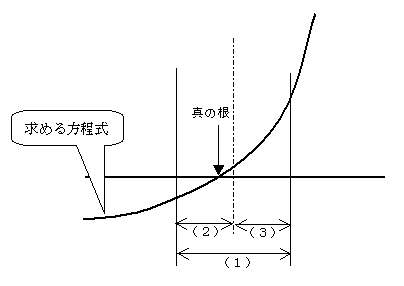 恾1
恾1
Newton method
戙悢揑側夝朄偑巊偊側偄応崌偵巊傢傟傞庤朄偺堦偮偱丄崻偺嬤帡抣偑暘偐偭偰偄傞応崌側偳偵桳岠偱丄廂懇偑懍偔岠棪揑側庤朄偱偡丅
婎杮揑側峫偊曽
揔摉側倶乽崻偺嬤帡抣偲梊憐偝傟傞抣佀乮侾乯乿偵懳偡傞摫娭悢梌偊偰摼傜傟傞愙慄偲倶幉偲偺岎揰傪媮傔傑偡丅佀乮俀乯
偦偺x偑丄慜偺抣傛傝恀偺崻偵嬤偄抣偲偟偰師偺愙慄傪媮傔偰丄倶幉偲偺岎揰傪媮傔傑偡丅佀乮俁乯
偙傟傪孞傝曉偟偰丄恀偺崻偺崻偵嬤偯偗偰峴偔庤朄偱偡丅
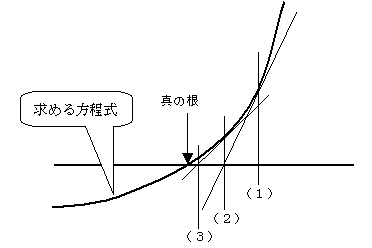 恾1
恾1
恖娫偺張棟擻椡傪忣曬検偱昞尰偟偰傒傞丅
乮侾乯尒偊傞忣曬傪僥儗價偺夋憸傪棙梡偟偰寁嶼偟偰傒傞丅
丂偁傞堦枃偺夋憸偑尰傟傞妋棪偼丄
丂P(偁傞堦枃偺夋憸) = 1 亐 (1夋慺偺怓悢) ^ 夋慺悢 = = 1 亐 (1夋慺偺怓悢) ^ (墶偺600丂亊 廲偺500)
丂1夋慺偺怓悢偼丄10抜奒 亊 3怓 偺 30 偱寁嶼偟偰傒傞丅
丂偙傟傛傝丄忣曬検 I 偼師偺傛偆偵側傞丅掙偼2偱寁嶼偟偰偄傞丅(懳悢偺岞幃棙梡)
丂I = - log P( 偁傞堦枃偺夋憸 ) = - log (1 亐 (30) ^ (600丂亊 500)) = (600丂亊 500) log 30 佮 1.5 亊 10^6 價僢僩
丂堦昩娫偵30枃掱搙尒傞偲峫偊傞偲丄1.5 亊 10^6 亊 30 = 4.5 亊 10^7 價僢僩/昩 掱搙偲尵偊傞丅
乮俀乯撉傒庢傝傗暦偒庢傝傪丄撉傓僗僺乕僪偐傜奣嶼偟偰傒傞丅
丂(2-1) 擔杮岅偼丄16亊16僺僋僙儖偱丄敀崟偲寁嶼偡傞偲侾暥帤偺忣曬検偼師偺傛偆偵寁嶼偱偒傞丅
丂I = - log ( 1 亐 2 ^(16亊16)) = - log 2^(-(16亊16)) = 256 價僢僩
(2-2) 傾儖僼傽儀僢僩側傜 5亊7僺僋僙儖偱丄忣曬検I = 35價僢僩
丂慜屻偺忣曬偐傜暯嬒忣曬検偼丄傕偭偲彮側偔傝丄幚幙偱偼12價僢僩掱搙偲偄傢傟傞丅丂
丂偦偟偰丄壖偵1昩娫偵10暥帤掱搙撉傔傞偲偡傞偲丄12 亊 10 = 120價僢僩/昩丂掱搙偵側傞丅
乮俁乯暦偙偊傞忣曬偺奣嶼
丂壒偺扨埵偵偼丄壒埑偺Pa乮僷僗僇儖乯傗壒埑儗儀儖偺db乮僨僔儀儖乯偑巊傢傟丄埲壓偵栚埨傪帵偡丅
| 恖娫偑暦偙偊傞尷奅偺壒丂 | 20Pa丂 | 1db |
| 偝偝傗偒惡丂 | 200Pa丂 | 40db |
| 夛榖 丂 | 20,000乣100,000Pa丂 | 60db乣70db |
| 旘峴婡偺壒丂 | 20,000,000Pa丂 | 120db(130db埲忋偼捝傒偵姶偠傞) |
丂側偍丄1Pa=1N/噓偱丄1N偼1Kg傪1m/昩^2 偺壛懍搙偱摦偐偡椡偱偁傞丅
丂壒埑儗儀儖偼師偺傛偆偵掕媊偝傟傑偡丅(log偺掙偼丄10乯
丂壒埑儗儀儖丂= 20 log (壒埑Pa亐恖娫偑暦偙偊傞尷奅抣Pa) = 20 log (壒埑Pa亐20Pa) [扨埵:db丂僨僔儀儖]
丂0乣60db偺斖埻偱埑椡偑尰傟傞帪偺暦偙偊傞妋棪偼丄20Pa亐20000Pa 偲偡傞偲丄偙偺忣曬検I偼師偺傛偆偵嶼弌偱偒傞偱偒傞偱偟傚偆丅
丂I = -log(20/20000) = -log10^-3 = 3亊log10 佮 3亊3.3 佮 10價僢僩
丂偝傜偵丄10KHz傑偱暦偙偊偰丄偦偺廃婜偱1價僢僩傪憲傟傞偲峫偊傞偲丄
丂10亊10^3 亊 壒埑忣曬偺10 = 10^5 價僢僩/昩丂丂掱搙偺忣曬張棟擻椡偲尵偊傞丅
乮係乯堄幆偡傞忣曬張棟
丂擼偺恄宱嵶朎(neuron)偱丄僔僫僾僗(synapse) 偲屇偽傟傞愙懕晹偱憲傜傟傞僷儖僗偑300僷儖僗/昩掱搙偲尵傢傟丄偙傟偑忣曬検偲尵偊傞偩傠偆丅
 恾1
恾1
Certificate Authority
憲傝庤偼丄帺恎旈枾偐偓偱夵偞傫偝傟傞偙偲偑側偄亀僨僕僞儖彁柤亁傪庴怣幰傊憲怣偱偒傞丅
丂偮傑傝丄庴怣幰懁偱偼丄憲怣幰偺岞奐偐偓傛傝暯暥偑夵偞傫偝傟側偰偄側偄偙偲偑傢偐傞栿偩丅
丂偟偐偟丄岞奐偐偓帺懱偵偼恖暔傪杮摉偵摿掕偡傞傕偺偼壗侾偮側偄丅岞奐偐偓偵傛偭偰杮摉偺恖暔傪摿掕偡傞偺偼崲擄偱偁傞丅
偙傟傪夝寛偡傞偨傔偺乽偐偓娗棟乿偺曽朄偺堦偮偲偟偰丄俀幰娫偱巊梡偡傞岞奐偐偓偺惓摉惈傪徹柧偡傞戞嶰幰偲偟偰偺婡娭偑昁梫偵側傞丅
偙傟偑擣徹嬊偱偁傞丅
崙撪偱偼丄擔杮傋傝僒僀儞亀http://www.verisign.co.jp/亁丄僒僀僶乕僩儔僗僩丄擔杮擣徹僒乕價僗側偳偑婡娭偑桳柤偱偁傞丅
擣徹嬊偺巇棤偼丄戝偒偔暘偗偰俀偮偁傞丅
丒岞奐偐偓偲偦偺岞奐偐偓偐扤偺傕偺偱偁傞偐傪徹柧偡傞徹柧彂傪敪峴偡傞偙偲丅
丂傑偢嵟弶偵僉乕儁傾乕乮旈枾偐偓偲岞奐偐偓乯傪惗惉偡傞丅堦斒偙偺惗惉偼倂倂倂僽儔僂僓乕撪晹偱峴偊傞丅
丂偦偟偰擣徹嬊偵岞奐偐偓偲偦偺岞暵偐偓偺惓摉惈傪徹柧偡傞傛偆側帺暘偺懏惈乮俙偝傫偺柤慜丄儊乕儖傾僪儗僗側偳乯傪堦弿偵憲傞偙偲偵側傞丅
丂偙傟偵懳偟偰擣徹嬊偱偼庴偗庢偭偨忣曬傪傕偲偵僨僕僞儖倢俢偲尵偆岞奐偐偓傪敪峴偡傞丅
丒搊榐偝傟偰偄傞岞奐偐偓偺栤偄崌傢偣偑戞嶰幰偐傜偁偭偨応崌偵丄偦傟傪徹柧彂晅偒偱憲晅偡傞偙偲丅
堦斒偵僨僕僞儖倢俢偼丄桳岠婜尷丄擣徹斣崋丄敪峴偟偨擣徹嬊柤偵壛偊丄搊榐幰偺懏惈乮柤慜丄儊乕儖傾僪儗僗側偳乯丄搊榐幰偺岞奐偐偓側偳偑
娷傑傟偰偄傞丅偙傟傜傪慻傒崌傢偣偨傕偺傪僴僢僔儞僌偟偰擣徹嬊偺旈枾偐偓偰埫崋壔偟偨偟偨傕偲側傞丅
偦偟偰丄偙偺擣徹嬊偺岞奐偐偓偼僽儔僂僓偵揧晅偝傟傞宍懺偵側傞丅
椺偊偽丄擣徹嬊偺戝庤偱偁傞儀儕僒僀儞幮偱偁傟偽丄俼俽俙僨乕僞僙僉儏儕僥傿乕幮偺採彞偡傞S/MIME偲偄偆埫崋捠怣曽朄傪巊偭偨
僱僢僩僗働乕僾僐儈儏僯働乕僞乕傗儅僀僋儘僜僼僩僀儞僞乕僱僢僩僄僋僗僾儘乕儔乕側偳偼丄昗弨偱偙偺岞奐偐偓偑揧晅偝傟偰偄傞丅
偙傟偵傛傝丄揹巕彁柤晅偒埫崋壔儊乕儖偺憲庴怣偱偼乽搻挳乿乽夵偞傫乿乽側傝偡傑偟乿偺偡傋偰偺婋尟傪夞旔偡傞偙偲偑偱偒傞丅
側偍丄偙偺応崌偺儊乕儖偺埫崋壔偵偼丄嫟捠偐偓埫崋偑巊傢傟傞丅偦傟偼嫟捠偐偓埫崋曽幃偼岞奐偐偓埫崋曽幃偵斾傋丄
埫崋壔偲暅崋壔張棟偑崅懍偱丄偟偐傕惗惉偝傟偨暥偺戝偒偝傕彫偄偨傔偱偁傞丅
偦偺偨傔丄儊乕儖慡懱傪庴怣幰偺岞奐偐偓偱埫崋壔偡傞庤朄偱側偔丄嫟捠偐偓偩偗傪庴怣幰偺岞奐偐偓偱埫崋壔偟丄
儊乕儖慡懱偼嫟捠偐偓偱埫崋壔偡傞丅
偙偺傛偆偵俀偮偺埫崋曽幃偺棙揰傪妶偐偡偙偲偵傛偭偰埨慡偱崅懍側張棟偐幚尰偝傟偰偄傞丅
側偍丄嫟捠偐偓偼憲怣偺偨傃偵怴偟偄傕偺偑惗惉偝傟傞丅
 yahoo
MSN
僄僉僒僀僩
Google
yahoo
MSN
僄僉僒僀僩
Google yahoo
MSN
僄僉僒僀僩
Google
yahoo
MSN
僄僉僒僀僩
Google 恾1
恾1 恾1
恾1 恾1
恾1