 yahoo
MSN
エキサイト
Google
yahoo
MSN
エキサイト
Google yahoo
MSN
エキサイト
Google
yahoo
MSN
エキサイト
Google 図1
図1 図2
図2
#include <stdio.h>
int a[] = {0,4,35,8,30,3,25,13,7,40,1,17,9,2,5,20}; //a[0]は使っていない
//配列(j〜end_idxの添え字範囲)で、j番目要素を頂点したヒープ構成へ変更にする。→j番目に最大値を移動
void heap(int a[], int j, int end_idx)
{
int i,v;
v = a[j];
while(j <= end_idx/2){
i = 2*j;
if(i < end_idx && a[i] < a[i+1]) i++; //大きい方を、a[i] で表現できるようにしている。
if(v >= a[i]) break;
a[j] = a[i];
j = i;
}
a[j] = v;
}
void heap_sort(int a[], int n) //nは個数でなく最後んp要素を指すインデックス
{
int j,t;
for(j = n/2; j >= 1; j--){
heap(a,j,n);
}
while(n > 1){
t = a[1]; a[1] = a[n]; a[n] =t; //交換
heap(a,1,--n);
}
}
void main()
{
int i, n = sizeof(a)/sizeof(a[0])-1;
heap_sort(a,n);
for(i = 1; i <= n; i++)
printf("%d ",a[i]);
printf("\n");
}
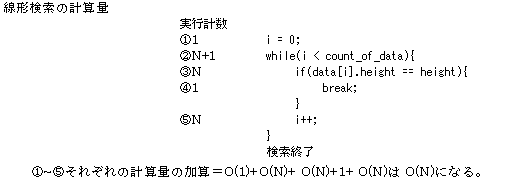 図1
図1 図2
図2| アルゴリズム | 最大計算量 | 平均計算量 |
| 線形探索 | n | n/2 |
| 二分探索 | 平均回数+1 | log2(N) |
| バブルソート | n^2 | n^2 |
| 選択ソート | n^2 | n^2 |
| 挿入法 | n^2 | n^2 |
| クイックソート | n^2 | n×log2(n) |
| ヒープソート | n×log2(n) | n×log2(n) |
| シェルソート | ? | n^(2/3) |
| はい | いいえ |
| 正 | 負 |
| 男 | 女 |
| スイッチのオン | オフ |
| 00 | なにも付けない |
| 01 | 赤色ライトをつける |
| 10 | 黄色ライトをつける |
| 11 | 青色ライトをつける |
| 000 |
| 001 |
| 010 |
| 011 |
| 100 |
| 101 |
| 110 |
| 111 |
| 000 | 0と決める |
| 001 | 1と決める |
| 010 | 2と決める |
| 011 | 3と決める |
| 100 | 4と決める |
| 101 | 5と決める |
| 110 | 6と決める |
| 111 | 7と決める |
| 000 | 0と決める |
| 001 | 1と決める |
| 010 | 2と決める |
| 011 | 3と決める |
| 100 | -4と決める |
| 101 | -3と決める |
| 110 | -2と決める |
| 111 | -1と決める |
┳━国際標準━┳━情報処理━ISO(International Organization for Standardization):国際標準化機構 ┃ ┃ ┃ ┣━電気━IEC(International Electrotechnical Commission):国際電気標準会議 ┃ ┃ ┃ ┗━電気通信━ITU(International-Telecommunication Union):国際-電気通信 連合 ┃ ┣━国内標準━┳米国━ANSI(American National Standards Institute):米国規格協会、EIA、TIA、UL規格会社、etc ┃ ┃ ┃ ┗日本┳情報処理━JIS(Japan Industrial Standard):日本工業規格 ┃ ┃ ┃ ┗電気通信━TTC標準(Telecommunication Technology Committee):社団法人情報通信技術委員会 ┃ ┣━業界標準━┳━インターネット━IETF(Internet Engineering Task Force) ┃ ┃ ┃ ┗━LAN━IEEE規格など ┃ ┗━技術標準━┳━フォーラム(公開討論)━ATM Forum、etc ┃ ┗━コンソーシアム(consortium:組合)━PCCA 米国移動通信機器メーカー組合など
 図1
図1| 変数T | 0.0000 | 0.0100 | 0.0200 | 0.0300 | 0.0400 | 0.0500 | 0.0600 | 0.0700 | 0.0800 | 0.0900 |
| 0.0000 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1000 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2000 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3000 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4000 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5000 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6000 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7000 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7703 | 0.7734 | 0.7764 | 0.7793 | 0.7823 | 0.7852 |
| 0.8000 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9000 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0000 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1000 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2000 | 0.8849 | 0.8869 | 0.8888 | 0.8906 | 0.8925 | 0.8943 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3000 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4000 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5000 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6000 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7000 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8000 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9000 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2.0000 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1000 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2000 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3000 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4000 | 0.9918 | 0.9920 | 0.9922 | 0.9924 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5000 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6000 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7000 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8000 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9000 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3.0000 | 0.9986 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |
| 3.1000 | 0.9990 | 0.9991 | 0.9991 | 0.9991 | 0.9992 | 0.9992 | 0.9992 | 0.9992 | 0.9993 | 0.9993 |
| 3.2000 | 0.9993 | 0.9993 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9995 | 0.9995 | 0.9995 |
| 3.3000 | 0.9995 | 0.9995 | 0.9995 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 |
| 3.4000 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9998 |
| 3.5000 | 0.9998 | 0.9998 | 0.9998 | 0.9998 | 0.9998 | 0.9998 | 0.9998 | 0.9998 | 0.9998 | 0.9998 |
| 3.6000 | 0.9998 | 0.9998 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 |
| 3.7000 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 |
| 3.8000 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 | 0.9999 |
| 3.9000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
