 yahoo
MSN
エキサイト
Google
yahoo
MSN
エキサイト
Google yahoo
MSN
エキサイト
Google
yahoo
MSN
エキサイト
Google| 名前 | 備考 | 記憶原理 |
| フラッシュメモリ利用のメディア | (RAMディスク) | 半導体(EEPROM) |
| 磁気テープ(Magnetic Tape Unit) | ランダムアクセス不可(オープンリールテープ方式とカートリッジ方式あり) | 磁気 |
| RAID | レイドと呼ぶ。ハードディスクを複数並べて管理する。 | 磁気 |
| ハードディスク | 主流は3.5インチ(ノートは2.5インチ) | 磁気 |
| ZIP | ジップと呼ぶ。高密度磁気リムーバブル | 磁気 |
| MO | 光磁気ディスク(Magnet Optical disk) | レーザー光と磁化ヘッドで書き込み、光の反射で読み取る。 |
| DVD-ROM、DVD-R、DVD+RW、DVD-RAM、CD-RW | 片面4.7GB | 凹凸をレーザー反射光で読み取る(反射率が小さい) |
| CD-ROM、CD-R、CD-RW | 700MB程度 | 凹凸をレーザー反射光で読み取る(反射率が大きい) |
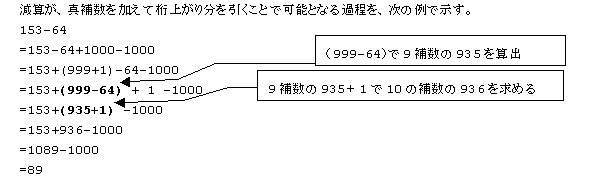 図1
図1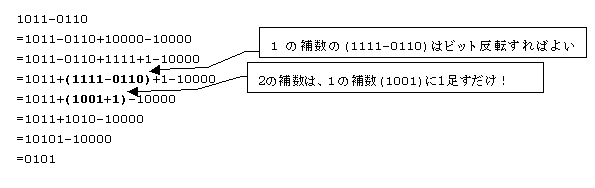 図2
図2| 擬補数(1の補数) | 全てのビットを反転するだけで求められる。 |
| 真補数(2の補数) | 上記1の補数に1を加えると求められる。そして、これが(−N)の負を記憶する方法になっている。 |